W dotychczas wykonanych analizach wykorzystaliśmy jedynie dwa rodzaje elementów: opornika (R) i kondensatora (C). Konieczne było również przedstawienie niezależnych źródeł napięć (V). Jednak SPICE umożliwia także użycie wielu innych komponentów. Wymieńmy tylko najważniejsze z nich: dioda (D), indukcyjność (L), indukcyjność wzajemna (K), tranzystor MOSFET (M), tranzystor JFET (J) czy tranzystor bipolarny (Q), [1]. Każdy z tych elementów ma w programie SPICE co najmniej jeden model, czyli opis matematyczny jego działania. Wykonanie analizy oznacza więc rozwiązanie szeregu równań wiążących, w najprostszym przypadku, napięcia i prądy elementów. Uwzględniana jest także temperatura panująca w układzie. Jak pamiętamy z omawianych do tej pory przykładów, pominięcie deklaracji wartości temperatury skutkowało wykonaniem symulacji dla domyślnej wartości 27°C (300 K). Ten fakt wskazuje nam, że modele elementów zawierają także zależności temperaturowe, ale i niekiedy zależności od aktualnej wartości napięcia czy prądu.
Modele elementów R, C i L
Rozpatrzmy na przykład modele rezystora. Ich pełne postaci to [1, 2]:
R(T)=R0·[1+TC1·(T-T0)+TC2·(T-T0)2+TC3·(T-T0)3+...],
lub
R(T)=R0·1,01TCE·(T-T0),
gdzie TC1, TC2, TC3 i TCE są współczynnikami temperaturowymi.
Z kolei model kondensatora jest opisany równaniem [1]:
C(T,V)=C0·[1+VC1·V+VC2·V2]·[1+TC1·(T-T0)+TC2·(T-T0)2],
gdzie TC1 i TC2 są współczynnikami temperaturowymi, a VC1 i VC2 to odpowiednio liniowy i kwadratowy współczynnik zależności pojemności od napięcia.
W taki sam sposób opisane jest zachowanie indukcyjności [1]:
L(T,V)=L0·[1+VL1·V+VL2·V2]·[1+TL1·(T-T0)+TL2·(T-T0)2],
gdzie współczynniki VL1, VL2, TL1 i TL2 są określone analogicznie jak te z modelu kondensatora.
Domyślne wartości współczynników temperaturowych i napięciowych są równe 0.
Podane powyżej zależności są ogólne i niestety nie są tak samo zaimplementowane w różnych wersjach SPICE-a. Na przykład w modelu rezystancji, LTspice pozwala na użycie jedynie dwóch współczynników temperaturowych: TC1 i TC2, a w przypadku modelu pojemności, ltwiki [2] nie podaje podobnej formuły na obliczanie wartości kondensatora jako funkcji temperatury i napięcia. Natomiast w symulacjach w LTspice Autorowi udało się wykorzystać jedynie jeden współczynnik - temperaturowy o nazwie TC, który opisuje liniową zależność od temperatury, o czym będzie mowa w dalszej części. Są to konsekwencje i jednocześnie dowody faktu, że różne wersje SPICE-a rozwijały się osobno i nie ma do końca spójności między nimi.
Analiza temperaturowa Temperaturę w układach elektronicznych można rozpatrywać z dwóch perspektyw. Pierwsza to jej wpływ na parametry układu. Oznacza to, ni mniej, ni więcej, że wykonany układ (np. procesor w odtwarzaczu mp3) musi działać poprawnie zarówno w zimie, przy temperaturze poniżej -20°C, jak i w czasie wycieczki na Saharę w samo południe, gry temperatura może sięgać nawet 50°C. Co więcej, ten sam procesor wykorzystany w komputerze o dużej mocy obliczeniowej powinien pracować poprawnie nawet dla ponad 100°C. Drugim aspektem jest awaryjność. Długotrwała praca w podwyższonej temperaturze przyczynia się do skrócenia bezawaryjnego czasu pracy MTBF (ang. Mean Time Between Failures).
Analizę wpływu temperatury definiuje się za pomocą dyrektywy .TEMP, a jej ogólna postać to [1]:
.TEMP T1 [T2 T3 …]
Podanie więcej niż jednej wartości temperatury spowoduje wykonanie serii obliczeń. Sama dyrektywa .TEMP nie określa rodzaju symulacji - jest to dyrektywa pomocnicza.
Aby lepiej zrozumieć omawiany temat, wykonajmy analizę wpływu temperatury na wartość rezystancji. Do tego celu użyjmy kilku oporników o rezystancji równej 10 V, jednak z różnorako sprecyzowanymi współczynnikami temperaturowymi (rysunek 1). Rezystor R1 niech pozostanie z domyślnymi wartościami. Natomiast kolejne oporniki mają następujące modyfikacje (współczynniki temperaturowe podajemy po wartości rezystancji): R2 10 tc1=-2e-4, R3 10 tc1=1e-4 tc2=-1e-5, R4 10 tce=0,05. Temperatura przyjmuje wartości od 0 do 100°C z krokiem 10°C. Jako symulację wybierzmy analizę punktu pracy .OP, a badane elementy niech będą zasilone stałym napięciem 1 V.
Netlista omawianego przykładu wygląda następująco:
* D:EPprzyk_3_01_1.asc
V1 VR 0 1
R1 VR 0 10
R2 VR 0 10 tc1=-2e-4
R4 VR 0 10 tce=0.05
R3 VR 0 10 tc1=1e-4 tc2=-1e-5
.TEMP 0 10 20 30 40 50 60 70 80 90 100
.op
.backanno
.end
Po wykonaniu symulacji klikamy na poszczególne rezystory, żeby wyświetlić wartości prądów przez nie płynących, które, zgodnie z prawem Ohma, są odwrotnie proporcjonalne do rezystancji. Aby dowiedzieć się, jaki dokładnie wpływ ma temperatura na oporniki, można pokusić się o użycie kursorów, odczytanie wartości prądów i dokonanie obliczeń przy wykorzystaniu wspomnianej proporcji.
Pomiary
Jednakowoż programy typu SPICE oferują nam pomoc w odczytywaniu, obliczaniu czy mierzeniu pewnych wielkości. Służy temu dyrektywa .MEASURE (oznaczająca pomiar, którą można też zapisać w skrócie .MEAS). W omawianym przykładzie wykorzystamy tę opcję do wykonania pomiaru pewnej wartości zmiennej niezależnej, a jest nią tutaj temperatura. Zastosowanie tej deklaracji pokażemy na przykładzie pomiaru rezystancji w omawianej analizie. Za pomocą ikonki do definiowania dyrektyw z oznaczeniem .op należy wprowadzić kolejno poniższe linie i umieścić je na schemacie (pojawią się one również w netliście):
.MEAS OP RES_3_0 FIND V(VR)/I(R3) AT=0
.MEAS OP RES_3_10 FIND V(VR)/I(R3) AT=10
.MEAS OP RES_3_20 FIND V(VR)/I(R3) AT=20
.MEAS OP RES_3_30 FIND V(VR)/I(R3) AT=30
.MEAS OP RES_3_40 FIND V(VR)/I(R3) AT=40
.MEAS OP RES_3_50 FIND V(VR)/I(R3) AT=50
.MEAS OP RES_3_60 FIND V(VR)/I(R3) AT=60
.MEAS OP RES_3_70 FIND V(VR)/I(R3) AT=70
.MEAS OP RES_3_80 FIND V(VR)/I(R3) AT=80
.MEAS OP RES_3_90 FIND V(VR)/I(R3) AT=90
.MEAS OP RES_3_100 FIND V(VR)/I(R3) AT=100
Słowo OP oznacza, że pomiar będzie dokonany podczas analizy .OP, nazwy RES_3_0, RES_3_10, … utworzono z nazwy rezystora R3 i dopełniono wartością temperatury. Słowo FIND pozwala na znalezienie (obliczenie) ilorazu napięcia w węźle VR i prądu płynącego przez opornik R3 (czyli de facto wartości rezystancji), gdy zmienna niezależna przyjmuje wartość sprecyzowaną wyrażeniem AT=wartość. Oczywiście zaleca się utworzenie podobnych pomiarów dla pozostałych rezystorów.
Obliczone podczas symulacji wartości zostaną zapisane w pliku log:
res_3_0: v(vr)/i(r3)=9.9001 at 0
res_3_10: v(vr)/i(r3)=9.9541 at 10
res_3_20: v(vr)/i(r3)=9.9881 at 20
res_3_30: v(vr)/i(r3)=10.0021 at 30
res_3_40: v(vr)/i(r3)=9.9961 at 40
res_3_50: v(vr)/i(r3)=9.9701 at 50
res_3_60: v(vr)/i(r3)=9.9241 at 60
res_3_70: v(vr)/i(r3)=9.8581 at 70
res_3_80: v(vr)/i(r3)=9.7721 at 80
res_3_90: v(vr)/i(r3)=9.6661 at 90
res_3_100: v(vr)/i(r3)=9.5401 at 100
Wyniki te są zgodne z otrzymanym na wykresie przebiegiem prądu I(R3). Początkowo wartość rezystancji rośnie, osiągając maksimum, a następnie maleje, wraz ze wzrostem temperatury.
LTspice ma ciekawą opcję. Po napisaniu samej deklaracji .MEAS i umieszczeniu jej na schemacie, możemy, poprzez kliknięcie na niej prawym przyciskiem myszy, otworzyć nowe okno, które umożliwi uzupełnianie definicji pomiaru (rysunek 2). Co więcej, znajduje się tam przycisk Test umożliwiający sprawdzenie działania tworzonego przez nas pomiaru.
Aby zweryfikować współczynnik temperaturowy pojemności, stwórzmy układ składający się z dwóch filtrów dolnoprzepustowych (rysunek 3). W pierwszym zarówno rezystor (1 kV), jak i kondensator (1 nF) są niezależne od temperatury, a w drugim jedynie pojemność ma wskazaną wartość współczynnika TC (C2 NC2 0 1n TC=1e-2). Pomiar wartości pojemności będzie dokonany pośrednio poprzez pomiar częstotliwości granicznych:
.MEAS AC fgr1 WHEN mag(V(NC1))=0.707
.MEAS C1val PARAM 1/(2*Pi*1k*fgr1)
.MEAS AC fgr2 WHEN mag(V(NC2))=0.707
.MEAS C2val PARAM 1/(2*Pi*1k*fgr2)
.opt meascplxfmt=polar
Pierwsza i trzecia linia zawierają pomiar częstotliwości granicznych. Podobnie jak poprzednio, słowo AC mówi, dla jakiego rodzaju analizy (tutaj .AC) wykonywany jest pomiar. Następnie podane są nazwy, pod którymi opisane zostaną wyniki, np. fgr1 - częstotliwość graniczna dla filtra utworzonego z rezystancji R1 i pojemności C1. W tych pomiarach wykorzystano warunek gdy (ang. when), który sprawdza, kiedy spełnione jest wyrażenie mag(V(NC1))=0.707, gdzie mag oznacza amplitudę (ang. magnitude). Czyli znajdź częstotliwość (zmienną niezależną), dla której amplituda V(NC1) wynosi 0.707 V. Z kolei druga i czwarta linia to nic innego, jak wykonanie obliczenia wartości pojemności ze wzoru na częstotliwość graniczną z poprzedniej części kursu. Niestety LTspice wynik pomiarów analizy AC podaje w decybelach (dB), co skutkowałoby wartością pojemności rzędu 20log(1n)=-180 dB (!). Dlatego zastosowano linię .opt meascplxfmt=polar, która zmienia opcję wyświetlania wyniku analizy jako moduł liczby i fazę [3]. Może to też nie jest idealne, ale można przynajmniej odczytać wartości pojemności z pliku log, którego część zawartości podano poniżej. (Należy w tym miejscu wspomnieć, że inne wersje SPICE-a nie mają tej wady i jako wynik otrzymamy po prostu szukaną liczbę). Dla pojemności C1 podano jedynie pierwsze linie wyników pomiarów (dla temperatury 0°C), ponieważ pozostałe są identyczne.
Measurement: fgr1
Step mag(v(nc1))=0.707
1 159255
…
Measurement: c1val
Step 1/(2*pi*1k*fgr1)
1 (9.99369e-010,0°)
…
Measurement: fgr2
Step mag(v(nc2))=0.707
1 218819
2 192108
3 171742
4 154723
5 141359
6 129657
7 119932
8 111706
9 104291
10 97764.1
11 92285
Measurement: c2val
Step 1/(2*pi*1k*fgr2)
1 (7.27336e-010,0°)
2 (8.28467e-010,0°)
3 (9.26711e-010,0°)
4 (1.02864e-009,0°)
5 (1.1259e-009,0°)
6 (1.2275e-009,0°)
7 (1.32705e-009,0°)
8 (1.42476e-009,0°)
9 (1.52607e-009,0°)
10 (1.62795e-009,0°)
11 (1.7246e-009,0°)
Dla potwierdzenia, że współczynnik TC wprowadza liniową zależność pojemności od temperatury, otrzymane wyniki zilustrowano na rysunku 4.
Modele raz jeszcze
Przykłady z rysunków 1 i 3 obrazują, jak modyfikować wartości wbudowane modelowanych parametrów dla każdego elementu z osobna, co może być uciążliwe w przypadku używania większej liczby tych komponentów. Jeżeli jednak wiemy, że dana rodzina elementów zachowuje się identycznie, możemy utworzyć dla niej odpowiedni model. Zdefiniujmy przykładowy model rezystora, w którym uwzględnimy współczynniki temperaturowe, a wartość oporu będzie podawana przy definicji elementu. Dokonujemy tego za pomocą deklaracji .model:
.model res_mod R (tc1=1e-4 tc2=-1e-5)
gdzie res_mod jest nazwą modelu, R jest typem elementu (w naszym przykładzie rezystorem), a w nawiasach podajemy nazwy definiowanych parametrów i ich wartości.
Przykład zastosowania tego modelu znajduje się na rysunku 5. Powyższą deklarację wprowadzamy podobnie jak inne, czyli za pomocą ikonki z opisem .op lub za pomocą skrótu klawiszowego S. Dla zwiększenia przejrzystości rysunku i samej symulacji analizę zmniejszono do sześciu wartości temperatury.
Żeby podać nazwę modelu, należy kliknąć na danym elemencie prawym przyciskiem myszy przy jednoczesnym wciśnięciu klawisza Ctrl. Pojawi się wówczas okno edycji atrybutów elementu (rysunek 6). Można też zaznaczyć, aby nazwa modelu była widoczna na schemacie (znak X pod napisem Vis. - visible).
Przedstawione na rysunku 5 charakterystyki obrazują taki sam wpływ temperatury na obydwa rezystory.
LTspice dostarcza biblioteki wielu elementów dostępnych na rynku, jak na przykład: diod czy tranzystorów MOSFET, JFET, bipolarnych. Znajdują się one w katalogu (jeśli korzystano ze standardowych ustawień podczas instalacji oprogramowania): C:UsersUserNameDocumentsLTspiceXVIIlibcmp.
Sposób dołączania do analizy takiego modelu zostanie zobrazowany na przykładzie wykonywania charakterystyk przejściowych i wyjściowych dyskretnego tranzystora MOSFET 2N7002. Tworzenie schematu rozpoczynamy od wstawienia tranzystora MOSFET, na przykład za pomocą skrótu klawiszowego F2. Klikamy w symbol prawym przyciskiem myszy i w oknie właściwości tranzystora wybieramy Pick New MOSFET (wybierz nowy tranzystor MOSFET), rysunek 7. Otworzy się nowe okno wyboru tranzystora MOSFET z dostępnej listy elementów, w którym odnajdujemy i wybieramy tranzystor 2N7002 (rysunek 8).
Następnie uzupełniamy schemat źródłami napięć stałoprądowych w każdej gałęzi pomiędzy końcówkami tranzystora i masą, przy czym wartości napięć VDS i VGS można ustawić na 1 V (te wartości będą zmieniane podczas analizy), a źródło napięcia w gałęzi dren-masa ma mieć wartość 0 V. Posłuży ono do pomiaru prądu wypływającego z drenu do masy (węzeł 0). By uzyskać charakterystyki przejściowe ID=ID(VGS), wykonujemy analizę stałoprądową .DC, w której najpierw deklarujemy zmianę źródła VGS, a następnie VDS, rysunek 9 i poniższa netlista do przykładu przyk_3_04.asc. Charakterystyki otrzymuje się poprzez kliknięcie na źródle napięcia Vidrain, co spowoduje wyświetlenie wartości prądu płynącego przez to źródło napięcia - czyli prądu drenu.
* D:EPprzyk_3_04.asc
VGS VG 0 1
VDS VD 0 1
Vidrain VS 0 0
M1 VD VG VS VS 2N7002
.model NMOS NMOS
.model PMOS PMOS
.lib C:UsersEPDocumentsLTspiceXVIIlibcmpstandard.mos
.dc VGS 0 10 0.1 VDS 0 10 1
.backanno
.end
Tranzystor MOSFET jest deklarowany za pomocą litery M jako pierwszego znaku w nowej linii netlisty:
Mnazwa_tranzystora_MOS węzeł_drenu węzeł_bramki węzeł_źródła węzeł_podłoża nazwa_modelu
W przypadku tranzystorów dyskretnych źródło i podłoże są ze sobą zwarte, dlatego w naszej netliście obie te końcówki są podłączone do węzła VS. Umieszczenie choćby jednego tranzystora MOSFET na schemacie powoduje, że LTspice automatycznie definiuje modele tranzystorów NMOS i PMOS. Za pomocą dyrektywy .LIB (skrót od library - biblioteka) dołącza on także odpowiednią bibliotekę z modelami tranzystorów. Znajduje się tam między innymi model wybranego urządzenia:
.model 2N7002 VDMOS(Rg=3 Vto=1.6 Rd=0 Rs=.75 Rb=.14 Kp=.17 mtriode=1.25 Cgdmax=80p Cgdmin=12p Cgs=50p Cjo=50p Is=.04p ksubthres=.1 mfg=Fairchild Vds=60 Ron=2 Qg=1.5n)
Tranzystory dyskretne są opisane za pomocą specjalnie przeznaczonego do tego celu modelu VDMOS (discrete vertical double diffused MOSFET transistor - dyskretny tranzystor pionowy MOSFET z podwójną dyfuzją). Dla odmiany tranzystory w układach scalonych są zdefiniowane tak zwanymi modelami monolitycznymi - zwykle czterokońcówkowymi (z osobnymi elektrodami źródła i podłoża).
Najważniejszymi parametrami tranzystora z izolowaną bramką są: jego napięcie progowe Vto, wewnętrzny parametr transkonduktancji Kp [1], pojemności pasożytnicze Cgd, Cgs, Cjo i rezystancja (między drenem a źródłem) włączonego tranzystora.
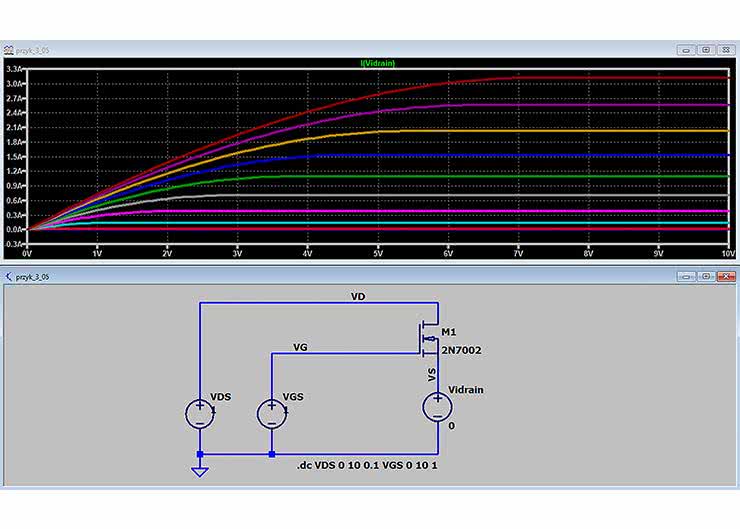
Aby uzyskać charakterystyki wyjściowe, w analizie .DC zamieniamy kolejność występowania źródeł (.dc VDS 0 10 0.1 VGS 0 10 1), rysunek 10.
Charakterystyki przejściowe i wyjściowe tego tranzystora zostały wykonane dla zakresu zmian napięć aż do 10 V, co daje prąd drenu większy niż 3 A i w rezultacie moc ponad 30 W. Przykładowe noty katalogowe tego elementu przewiduje napięcie VDS nawet do 60 V, ale maksymalną moc na poziomie od 0,2 W [4] do 0,83 W [5] (w zależności od producenta), której w rzeczywistym układzie nie wolno przekroczyć, aby nie uszkodzić tranzystora.
Podsumowanie
Analiza wpływu temperatury jest definiowana za pomocą deklaracji .TEMP:
.TEMP T1 [T2 T3 …]
przy czym wartości podawane są w stopniach Celsjusza. Temperatury niższe niż -223°C są pomijane. Nominalna wartość temperatury TNOM jest równa 27°C (są wersje SPICE-a dla których ta temperatura jest równa 25°C) i może być zmieniona za pomocą dyrektywy .OPTIONS (opcje).
Deklaracja .MEAS lub .MEASURE służy do znajdowania lub obliczania niektórych wartości. Mogą to być wartości pewnych zmiennych uzyskane w konkretnym czasie lub ogólniej zmiennej niezależnej. Takie przykłady były wykorzystane w tej części kursu i mogą być bardziej uniwersalnie zapisane jako
.MEAS analiza nazwa [FIND <wyrażenie>] [WHEN <wyrażenie>] [AT <wyrażenie>],
gdzie analiza oznacza rodzaj wykonywanej symulacji, jednak podawanej bez poprzedzającej ją kropki, np. OP, TRAN; nazwa oznacza zmienną, która przyjmie obliczaną wartość. FIND pozwala na wyszukanie wartości wyrażenia w czasie lub innej zmiennej niezależnej zdefiniowanej słowem AT. W następnych odcinkach poznamy również inne postaci tej deklaracji.
Komenda .OPTIONS, lub .OPTION, lub .OPT pozwala na ustawianie różnych parametrów, ograniczeń lub innych opcji w programie SPICE.
.OPTIONS [nazwa_opcji=wartość] [nazwa_opcji]
Występują opcje, które wymagają podania wartości, np.: .OPTIONS TNOM=20 (zmiana nominalnej temperatury na 20°C), a także takie, które występują same, np.: .OPTIONS NOOPITER zmienia metodę obliczania punktu pracy (podczas analizy .OP).
Dyrektywa
.MODEL nazwa typ [parametr=wartość …]
służy do definiowania modelu elementu. Jego nazwa musi być unikalna, typ definiuje rodzaj elementu, np. D - dioda, R lub RES - rezystor, NMOS - tranzystor polowy z izolowaną bramką typu N.
Ciekawostka
Dzięki uprzejmości firmy Silicon Creations, w której pracuję, miałem zaszczyt wziąć udział w konferencji ISSCC 2019 (International Solid-State Circuits Conference) poświęconej elektronicznym układom półprzewodnikowym [6]. Jest to najważniejsza konferencja organizowana przez inżynierów zrzeszonych w międzynarodowym stowarzyszeniu IEEE Solid-State Circuits Society, (z kolei skrót IEEE - Institute of Electrical and Electronics Engineers oznacza Instytut Inżynierów Elektryków i Elektroników).
Instytut IEEE corocznie przyznaje nagrody w wielu dziedzinach elektroniki, elektryki i informatyki. W tym roku nagroda oddziału Solid-State Circuits Society, mająca nazwę Donald O. Pederson Solid-State Circuits Award, została przyznana twórcy SPICE-a - Laurence’owi Nagelowi (na fotografii 11) za rozwój i ukazanie SPICE-a jako narzędzia do projektowania i optymalizacji układów elektronicznych [7]. Prawdopodobnie żaden inny wynalazek, wytwór czy osiągnięcie nie miało aż tak dużego wpływu na przemysł mikroelektroniczny jak SPICE, który został wykonany przez Nagela w czasie jego studiów na Uniwersytecie Kalifornijskim w Berkeley (University of California, Berkeley). SPICE przeniósł bazujące na doświadczeniach i prototypach projektowanie układów do ery symulacji i modelowania opartych na nauce. Nagel zaimplementował analizy czasowe, szumowe, a także stało- i zmiennoprądowe. Program ten był od samego początku ogólnodostępny, pozwalając na naukę działania układów bez konieczności ich budowy, a także na łatwe szukanie innych rozwiązań. Dzisiaj tworzenie układów, które nierzadko składają się z milionów tranzystorów, byłoby niemożliwe bez szczegółowych analiz, które udostępnia SPICE [7]. Na fotografii 12 pokazano budynek Inżynierii Elektrycznej wydziału EECS (Electrical Enginieering and Computer Science).
Adam Gołda
Bibliografia:
- J. Porębski, P. Korohoda, SPICE program analizy nieliniowej układów elektronicznych, WNT 1996
- http://bit.ly/2FyeAto, marzec 2019
- http://bit.ly/2uzJU5P, marzec
- http://bit.ly/2JK4St5
- http://bit.ly/2Uf05nL
- http://bit.ly/2uALS6e, marzec 2019
- http://bit.ly/2TCN3fr, marzec 2019

 Zaloguj
Zaloguj