Nie ma chyba elektronika, który nie zmierzyłby się z problemami związanymi z szeroko rozumianą stabilnością. Objawami jej braku jest tendencja do oscylacji lub przerzutów sygnału wyjściowego obserwowanych dla wymuszeń impulsowych. Równie dobrze pojęcie to jest znane automatykom. Opis zjawiska jest ogólny, a zastosowanie go do konkretnego przypadku zależy od interpretacji czynników występujących w formułach matematycznych.
Teoria opisująca zagadnienia związane ze stabilnością jest dość złożona. Trudno będzie wyczerpać temat w jednym odcinku cyklu. Zostaną więc przedstawione najbardziej istotne informacje w możliwie skondensowanej postaci.
Objawy niestabilności
Rozpatrywanie zagadnienia zaczniemy wyjątkowo od praktyki, nie od teorii. W układach ze wzmacniaczami operacyjnymi zasilanymi jednym napięciem często konieczne jest wytworzenie tzw. sztucznej masy, czyli napięcia równego połowie napięcia zasilającego. Zastosowanie prostego rezystancyjnego dzielnika napięciowego nie sprawdza się, gdyż impedancja wyjściowa układu musi być mała, najlepiej równa zero. Tymczasem rezystory dzielnika mają wartości rzędu kilku–kilkudziesięciu kiloomów. Konieczny jest więc bufor o małej impedancji wyjściowej. Najczęściej jest on budowany z użyciem wzmacniacza operacyjnego. W naszym przypadku będzie to układ OP491. Przykładowe rozwiązanie zostało pokazane na rysunku 1.
Sprawdźmy, czy rzeczywiście na wyjściu występuje napięcie równe 2,5 V przy założeniu, że napięcie zasilające jest równe 5 V. Uruchamiamy symulację Transient z czasem 200 mikrosekund i włączoną opcją „Start external DC supply voltages at 0V” (rysunek 1). Dzięki niej obserwujemy przebieg od chwili włączenia zasilania. Wynik symulacji potwierdza, że faktycznie na wyjściu uzyskujemy napięcie równe połowie napięcia zasilającego. Dokładniej mówiąc – napięcie wynikające ze stosunku rezystancji dzielnika R1 i R2, ale w naszym przypadku są one równe, więc napięcie jest dzielone na pół.
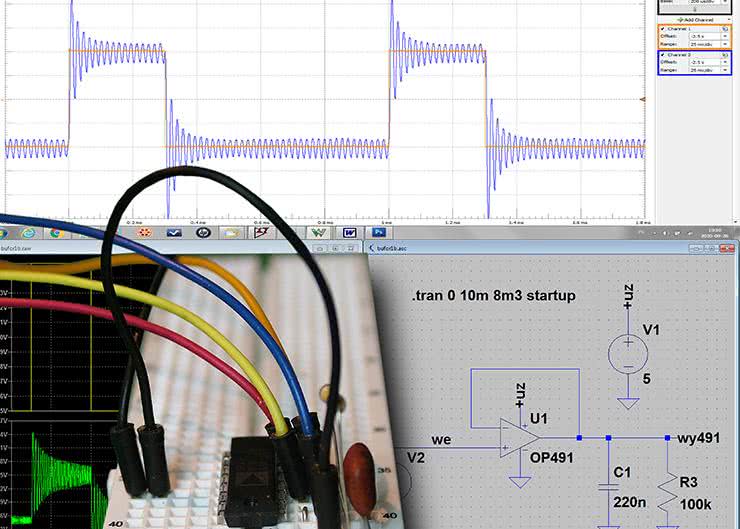
Wygląda na to, że układ pracuje zgodnie z założeniami, z tym że jest on nieobciążony. W praktyce oczywiście tak nie będzie, zobaczmy więc, co będzie się działo, gdy do wyjścia dołączymy obciążenie składające się z rezystancji np. 100 kV i pojemności 100 nF. Taki charakter będzie wykazywała większość układów rzeczywistych. Różnice mogą dotyczyć ewentualnie wartości rezystancji i pojemności. Należy jednak zauważyć, że wyjście bufora jest zawsze blokowane kondensatorami, występują ponadto jakieś pojemności montażowe, które decydują o pojemnościowym charakterze obciążenia. Symulowane napięcie wyjściowe pokazano na rysunku 2. Tym razem już tak ładnie nie jest. Pojawiły się niepożądane, na szczęście gasnące oscylacje (tak przynajmniej wydaje się na podstawie zgrubnej obserwacji) o częstotliwości ok. 229 kHz (rysunek 3). Aby sprawdzić, czy rzeczywiście gasną one do zera, wykonamy jeszcze jedną symulację Transient. Uruchamiamy ją komendą .TRAN 0 50m 49.98m startup, co oznacza że obserwujemy 20-mikrosekundowy fragment przebiegu oddalony o 49,98 milisekundy od chwili włączenia zasilania (rysunek 4). Okazuje się, że oscylacje nie gasną do zera, a utrzymują się na poziomie ok. 44,4 mVpp i mają częstotliwość ok. 281 kHz. Czyżbyśmy mieli jakiś problem ze stabilnością? Trochę nie dowierzając, sprawdzamy układ rzeczywisty. Jego schemat jest dokładnie taki sam jak w symulacji, a do pomiaru tradycyjnie używamy zestawu Analog Discovery 2.
Najpierw sprawdzimy fazę rozruchową. Do pomiaru potrzebny będzie oscyloskop i zasilacz +5 V. Po wstępnych próbach okazało się, że zasilacz AD2 nie jest tak idealny jak w symulacji. Czas ustalania się napięcia wynosi ok. 16 ms (rysunek 5). Chwilę przed osiągnięciem znamionowego napięcia pojawia się niewielki przerzut, po którym widoczne są jeszcze wyraźne dwa piki napięciowe i dalej można już uznać, że napięcie pozostaje stabilne. Zgoła odmiennie zachowuje się nasz bufor. Powtarza on oczywiście wspomniane wahania napięcia zasilającego, ale już po jego narośnięciu do ok. 0,8 V na wyjściu bufora zaczynają być widoczne wyraźne oscylacje. W stanie, który można uznać za ustalony, mają one amplitudę ok. 1 mVpp i częstotliwość 79 kHz. Zachowanie bufora nie odpowiada więc idealnie symulacji, chociaż jak z niej wynikało, układ rzeczywisty również nie jest w pełni stabilny. Drgania są na szczęście dużo mniejsze, mniejsza też jest ich częstotliwość.
Niestabilność układu można łatwo diagnozować, badając jego odpowiedź na małosygnałowe wymuszenie impulsowe. Sprawdźmy, jak taki test będzie wyglądał w przypadku naszego bufora. W tym celu dołączamy do wejścia nieodwracającego generator wytwarzający przebieg impulsowy o amplitudzie 20 mVpp ze składową stałą równą 2,5 V (połowa napięcia zasilającego). Schemat układu symulowanego, który następnie będzie mierzony jako układ rzeczywisty, pokazano na rysunku 6. Bufor jest kolejno obciążany pojemnościami 100 pF, 1 nF i 47 nF. Jak widać na wykresie uzyskanym w symulatorze, dla pojemności 100 pF i 1 nF widoczny jest przerzut napięcia wyjściowego i niewielkie, szybko gasnące drgania. Pojemność 47 nF powoduje powstanie drgań znacznie większych i wolniej gasnących. Wyjaśnienia wymaga sposób utworzenia wykresu widocznego na rysunku 6. Na wstępie utworzono 5 paneli przez kliknięcie prawym przyciskiem myszki w obszarze wykresu i wybranie polecenia „Add Plot Pane”. Następnie, po uaktywnieniu pierwszego panelu wstawiono do niego przebieg wejściowy, klikając na schemacie na węzeł opisany etykietą „we”. Tą samą metodą do kolejnych paneli wstawiono przebieg wyjściowy. Teraz, po uaktywnieniu drugiego panelu wybrano przebieg wyjściowy dla kondensatora 100 pF. Robimy to, klikając w obszarze panelu prawym przyciskiem myszki i wybierając polecenie „View→Select Steps”, a następnie podświetlamy pierwszą pozycję z wyświetlonej tabeli. Ważne jest, aby wyłączyć przy tym opcje: „Auto Range” i „Apply to All Panes”.
Podobnie postępujemy przy wstawianiu kolejnych dwóch wykresów dla pojemności 1 nF i 47 nF. Ostatni wykres jest utworzony z inną skalą czasową, aby pokazać przebieg wyjściowy dla pojemności 47 nF w szerszym zakresie. Skalę ustawiamy, klikając prawym przyciskiem myszki w obszarze dolnego panelu, a następnie wybierając opcje „View→Manual Limits”. Następnie należy ręcznie wprowadzić żądane wartości w pola grupy „Horizontal Axess”.
Mamy już wyniki symulacji, jest to dobry moment do weryfikacji praktycznej. Montujemy układ, uruchamiamy generator arbitralny, zasilacz i oscyloskop zestawu Analog Discovery 2. Korzystamy z 1. kanału generatora. Wybieramy przebieg prostokątny, ustawiamy częstotliwość 500 Hz, amplitudę 50 mV, offset 2,5 V i symetrię 14,8%. Przebieg wyjściowy obserwujemy w 2. kanale oscyloskopu. Ustawiamy w nim czułość 250 mV/dz i offset –1,5 V. Konieczne jest jeszcze włączenie okna Zoom, w którym wygodnie obserwujemy i mierzymy parametry oscylacji (rysunek 7). Zgodnie z przewidywaniami występują one w układzie rzeczywistym, chociaż mają nieco inne parametry niż w symulacji. Pomiary zaczynamy od dołączenia do wyjścia kondensatora 47 nF i powtarzamy dla następnych pojemności (1 nF i 100 pF). Po każdej zmianie kondensatora na wyjściu zapisujemy przebieg wyjściowy (z kanału 2.) jako referencyjny. W ten sposób tworzymy kolekcję pomiarów. Największe drgania występują dla pojemności 100 pF – amplituda 234 mVpp, częstotliwość 424 kHz. Wyniki pomiaru przedstawiono na rysunku 7.
Od praktyki do teorii
Wiemy już, że nasz układ – bufor wzbudza się. Pytanie dlaczego? Aby na nie odpowiedzieć, konieczna będzie ogólna analiza układów ze sprzężeniem zwrotnym. Podstawowy schemat blokowy układu ze sprzężeniem zwrotnym pokazano na rysunku 8. Na razie jest nieistotne, czy to układ elektroniczny, czy jakikolwiek inny, chociaż symbolika sygnałów może coś sugerować. Podstawowym elementem układu jest blok wzmacniający o wzmocnieniu K. Wzmacnia on K-krotnie sygnał Ur podawany do jego wejścia. Sygnał wyjściowy Uwy jest opisany zależnością:
Sygnał wyjściowy jest podawany z powrotem do wejścia przez blok β i węzeł sumacyjny. Sumowanie odbywa się jednak ze znakiem minus. W ten sposób realizowane jest ujemne sprzężenie zwrotne. Transmitancja pętli sprzężenia zwrotnego jest wyznaczona parametrem β, zwanym też współczynnikiem sprzężenia. Transmitancja ta pozwala określić, jaka część sygnału wyjściowego jest podawana do węzła sumacyjnego sprzężenia zwrotnego. Zależność opisująca sygnał sprzężenia zwrotnego Uf jest następująca:
Sygnał podawany na wejście wzmacniacza jest równy:
Wstawiając tę zależność do wzoru (1), otrzymujemy:
Po dalszych przekształceniach otrzymujemy:
Wzór (2) jest bardzo dobrze znany wszystkim inżynierom zajmującym się układami z ujemnym sprzężeniem zwrotnym. Określa całkowite wzmocnienie z zamkniętą pętlą sprzężenia zwrotnego. Wzmocnienie samej pętli jest równe Kβ.
Sprawdźmy, czy nasz bufor spełnia opisane wyżej kryteria. Blokiem wzmacniającym jest wzmacniacz operacyjny o wzmocnieniu w otwartej pętli równym K. Parametr ten jest na ogół podawany w danych katalogowych. Blok sprzężenia ma wzmocnienie β=1, gdyż napięcie wyjściowe jest podawane bezpośrednio na wejście odwracające. Węzeł sumacyjny jest realizowany przez wejściowy wzmacniacz różnicowy wzmacniacza operacyjnego (rysunek 9).
Zauważmy, że dla bardzo dużych wartości K, a tak jest w rzeczywistości, gdyż wzmocnienie wzmacniaczy operacyjnych w otwartej pętli jest rzędu 105...106, całkowite wzmocnienie układu z zamkniętą pętlą jest równe odwrotności wzmocnienia pętli sprzężenia zwrotnego:
Gdzie tkwi zagrożenie?
Wyrażenie (2) jest ułamkiem, którego mianownik jest równy: 1+Kβ. Nie trzeba mieć wielkiej wyobraźni, aby zadać pytanie: co się stanie, gdy czynnik Kβ będzie miał wartość –1? Ci, którzy ją mają, powiedzą: wzmacniacz sam wysadzi się w powietrze, gdyż jego wzmocnienie wzrośnie do nieskończoności. Oczywiście tak nie będzie. Nie pozwolą na to fizyczne ograniczenia wynikające choćby z wartości napięcia zasilającego. Zamiast takiej tragedii sygnał wyjściowy osiągnie możliwą wartość maksymalną i mógłby w niej pozostać, ale bardziej prawdopodobne jest wpadnięcie w oscylacje, gdyż wewnętrzne układy kompensujące i ograniczające będą dążyły do zmniejszenia sygnału wyjściowego, a wzmacniacz dalej będzie je wzmacniał.
No dobrze, ale aby mianownik osiągnął wartość zero, wzmocnienie pętli musi być ujemne, a w naszym przypadku β jest przecież równe 1, zaś sygnał wejściowy jest podawany na wejście nieodwracające, zatem wzmocnienie też jest większe od zera. Jest to jednak przypadek ogólny. W rzeczywistości wzmacniacze operacyjne są konstruowane tak, aby odpowiednio zaprojektowane układy kompensacji zapewniały stabilną pracę w aplikacjach praktycznych. Skutkuje to wprowadzeniem dominującego bieguna transmitancji wzmacniacza, który ogranicza maksymalne wzmocnienie zaledwie do kilku, kilkunastu, najwyżej kilkudziesięciu herców. Po przekroczeniu tej częstotliwości charakterystyka wzmocnienia spada z szybkością 20 decybeli na dekadę. Zmienia się też przesunięcie fazowe sygnału wyjściowego. To właśnie ten parametr wpływa na możliwość zmiany znaku wyrażenia Kβ. Należy je bowiem traktować jako liczbę zespoloną. Przy przesunięciu fazowym równym 180° wzmocnienie pętli jest równe –1, więc układ traci stabilność. Wykres wzmocnienia w otwartej pętli układu OP491 pokazano na rysunku 10. Niestety został on sporządzony, począwszy od częstotliwości 100 Hz i nie widać na nim bieguna dominującego. Zakładając, że maksymalne wzmocnienie układu jest równe ok. 96 dB (co można wywnioskować z tabeli zawierającej dane techniczne), przedłużamy prostą wzmocnienia (niebieska linia) do przecięcia z poziomem 96 dB i mierzymy częstotliwość tak wyznaczonego bieguna. Wynosi ona w przybliżeniu 47 Hz. Wyraźnie widzimy, że krzywa opada z szybkością 20 decybeli na dekadę. Cechę tę wykazuje większość popularnych wzmacniaczy operacyjnych. Niekiedy można dopatrzyć się drugiego bieguna charakterystyki, ale występuje on dopiero przy częstotliwościach megahercowych.
Na podstawie powyższych rozważań można wysnuć jeden bardzo ważny, wręcz fundamentalny wniosek gwarantujący bezpieczną pracę wzmacniacza: wzmocnienie pętli sprzężenia zwrotnego musi spełniać warunek:
Jak blisko wybuchu jesteśmy, czyli margines fazy i wzmocnienia
Transmitancję bloku sprzężenia zwrotnego dobieramy tak, aby po zamknięciu pętli uzyskać żądane wzmocnienie. Z oczywistych powodów charakterystyka wzmacniacza będzie zawsze przebiegała pod charakterystyką wzmacniacza z otwartą pętlą. Przykładowe wykresy asymptotyczne przedstawiono na rysunku 11.
Krytyczne warunki są osiągane, gdy Kβ=–1, co można zapisać również jako Kβ=1 przy przesunięciu fazowym 180°. Wynika z tego, że K=1/β. Jeśli oba parametry przedstawimy na wykresie ze skalą decybelową (rysunek 12), to operacji dzielenia odpowiada wówczas odejmowanie logarytmów:
Powróćmy do naszego bufora. Transmitancja jego pętli sprzężenia zwrotnego jest równa 1 (0 dB). Wykreśloną ją niebieska linią na rysunku 12. Do szybkiego określania niebezpieczeństwa utraty stabilności można posłużyć się szybkością zbliżania się charakterystyk. Szybkość opadania charakterystyki wzmacniacza z otwartą pętlą jest równa –20 dB/dek., zaś parametr ten dla pętli sprzężenia zwrotnego jest równy 0 dB/dek. Szybkość zbliżania charakterystyk co do wartości bezwzględnej jest równa:
Jeśli parametr ten jest mniejszy lub równy 20 dB/dek. mamy do czynienia z układem stabilnym, jeśli osiąga on wartość większą lub równą 40 dB/dek., to układ jest potencjalnie niestabilny.
Biorąc pod uwagę powyższy wniosek można sądzić, że niestabilność wystąpi w układzie, którego transmitancja będzie miała zero położone przed ociągnięciem punktu B. Przykład charakterystyki takiego układu przedstawiono na rysunku 13. Szybkość zbliżania się charakterystyk jest w tym przypadku równa:
Faktycznie, mamy więc układ potencjalnie niestabilny.
Rozważając zagadnienia związane ze stabilnością układów ze sprzężeniem zwrotnym, bardzo często odwołujemy się do dwóch parametrów określających, na ile groźna może być w danym przypadku utrata stabilności. Pierwszy parametr to margines fazy (rysunek 14). Określa on różnicę między rzeczywistą fazą układu a teoretyczną wartością, przy której powstają oscylacje, czyli 180°. Różnica ta jest mierzona w punkcie, w którym wzmocnienie jest równe 1 (0 dB). Drugi przypadek to margines wzmocnienia. Jest on mierzony w punkcie, w którym faza jest równa 180° i podaje, o ile wzmocnienie to różni się w odniesieniu do 0 dB.
Dlaczego bufor oscyluje?
Jako że obwód sprzężenia zwrotnego naszego bufora jest złożony ze zwykłego połączenia kawałka przewodnika, jego transmitancja jest równa 1. Odpowiednim dla tego przypadku wykresem będzie ten z rysunku 12. Szybkość zbliżania się charakterystyk jest równa co do modułu 20 dB/dek., zatem układ powinien być stabilny. Dlaczego więc oscyluje?
Aby odpowiedzieć na to pytanie, musimy wniknąć do wnętrza wzmacniacza operacyjnego (rysunek 15). Zakładamy, że wzmacniacz jest obciążony jakąś pojemnością CL. Jak już było wspomniane, stanowią ją chociażby pojemności pasożytnicze występujące w obwodzie rzeczywistym (pojemności wyprowadzeń, ścieżek obwodu drukowanego itp.), ale przede wszystkim dołączany zwykle do wyjścia bufora kondensator. Sygnał wyjściowy jest w tym modelu ukryty wewnątrz układu scalonego, a dostęp do niego mamy przez rezystancję wyjściową wzmacniacza ro oraz rezystancję doprowadzeń. W rzeczywistości obwód pętli sprzężenia zwrotnego będzie więc składał się z oporności ro, pojemności CL i połączenia (zakładamy, że idealnego) wyjścia układu z wejściem we–.
Transmitancja układu jest równa:
Wzmocnienie układu z zamkniętą pętlą jest równe:
Jak widać, transmitancja Kf ma jedno zero dla częstotliwości
co spowoduje załamanie charakterystyki 1/β – niestety w górę. Już wiemy, czym to grozi. Jeśli częstotliwość zera wypadnie przed przecięciem się charakterystyk z otwartą i zamknięta pętlą, tak jak na rysunku 13, możemy spodziewać się kłopotów z utrzymaniem stabilności układu. Czy jest jakaś metoda, aby takiemu przypadkowi zaradzić?
Przykładowa metoda eliminacji zera transmitancji
Skoro transmitancja 1/β ma niepożądane zero, to niemal intuicyjnie nasuwa się pomysł wprowadzenia elementu, który dodawałby do tej transmitancji kompensujący biegun. Rozważmy schemat z rysunku 16. Sprawdźmy, czy takim elementem jest rezystor Rs?
Transmitancja pętli sprzężenia zwrotnego jest równa:
Wzmocnienie układu z zamkniętą pętlą jest więc równe:
Zero i biegun różnią się o czynnik ro w stałej czasowej, przy czym występuje on w liczniku. Zatem częstotliwość zera, jako wielkość proporcjonalna do odwrotności stałej czasowej, wystąpi przed częstotliwością bieguna. Charakterystyka zakrzywi się więc w zerze do góry i zaraz potem zagięcie to zostanie zlikwidowane przez biegun. Jeśli z odgięciem charakterystyki zdążymy przed przecięciem się charakterystyk, zapewnimy stabilność układu.
Sprawdźmy w symulacji, czy zastosowanie tej metody ma szanse powodzenia? Testowanie wykonamy nie na modelach elementów z biblioteki LTspice, lecz na własnych modelach matematycznych. Skoro planujemy korzystać z aparatu matematycznego, to oczywiście będziemy musieli przypomnieć sobie przekształcenia Laplace’a i praktyczne ich stosowanie w symulatorze. Być może trzeba będzie wrócić do 12. odcinka cyklu, w którym zagadnienia te były opisane.
Zaczynamy od modelu wzmacniacza operacyjnego OP491, którego używamy w pomiarach układów rzeczywistych. Z danych katalogowych odczytujemy, że wzmocnienie jednostkowe (GBP – Gain Bandwidth Product) jest osiągane dla częstotliwości 3 MHz. Z danych katalogowych wnioskujemy też (nie jest to podane wprost), że wzmocnienie w otwartej pętli jest równe ok. 96 dB, czyli 63095 V/V. Na podstawie tych informacji szacujemy częstotliwość bieguna na 47 Hz. Przyjmując jednobiegunowy model charakterystyki możemy zapisać transmitancję układu OP491 dla pracy z otwartą pętlą jako:
Model matematyczny skompensowanego bufora już mamy (3). Występuje w nim parametr ro. Odczytujemy go z danych katalogowych wzmacniacza OP491 – Open-loop impedance = 200 V. Mamy komplet danych, możemy uruchamiać symulację. Będzie to badanie charakterystyki częstotliwościowej: .ac oct 100 1 10000k. Obliczenia transformaty Laplace’a prowadzimy za pomocą źródeł napięciowych sterowanych napięciowo (rysunek 17). W ich właściwościach w polu „Value” wpisujemy matematyczny zapis transmitancji. Wartości CL, ro i Rs zapisujemy parametrycznie, aby w razie konieczności można było łatwo je zmieniać. Przyjmujemy, że rezystor Rs będzie miał oporności 3 i 15 V, a pojemność CL jest równa 220 nF.
Jak widać z wykresów, dla rezystora Rs=3 V kompensacja wypadła poza punktem przecięcia się z charakterystyką wzmacniacza operacyjnego. Układ ten będzie więc niestabilny. Dla rezystancji Rs równej 15 V zdążyliśmy skompensować układ przed przecięciem z charakterystyką OP491, układ powinien być stabilny. Sprawdźmy to w praktyce.
Praktyczne sprawdzenie skuteczności kompensacji
Testowany układ montujemy na płytce stykowej zgodnie ze schematem widocznym na rysunku 18. Tak jak poprzednio wybieramy przebieg prostokątny o częstotliwości 500 Hz, amplitudzie 50 mV, offsecie 2,5 V i symetrii 7,3%. Przebieg wyjściowy obserwujemy w 2. kanale oscyloskopu. Początkowo ustawiamy w nim czułość 50 mV/dz i offset –2,5 V.
W układzie rzeczywistym rezystor Rs będzie się składał z kolejno dołączanych szeregowo rezystorów 3,3 V, aby sprawdzić, jak rezystancja ta wpływa na stabilność bufora. Kolejne wyniki będą zachowywane jako przebiegi referencyjne.
Pomiary potwierdziły, że powyżej 10 omów udaje się wygasić drgania na wyjściu bufora. Znacznie trudniejsza okazała się eliminacja przerzutu sygnału wyjściowego. Do skutecznego pozbycia się tego efektu konieczne było dołączenie rezystora ok. 100 V. Wyniki pomiarów czasowych przedstawiono na rysunku 19. Przebiegi dla kolejnych wartości rezystora Rs zostały rozsunięte tak, aby można je było wygodnie porównywać.
Jednocześnie z oglądaniem odpowiedzi bufora na pobudzenie impulsowe po każdej zmianie rezystancji Rs zmierzymy charakterystykę częstotliwościową, korzystając oczywiście z narzędzia Network zestawu Analog Discovery 2. I w tym przypadku każdy pomiar zachowamy jako przebieg referencyjny, aby możliwe było łatwe porównanie charakterystyk. Pamiętamy, że po włączeniu narzędzia Network odłączany jest generator arbitralny, a parametry sygnału testowego muszą być ustawione w oknie „Wavegen”. Do testu zawsze jest używany sygnał sinusoidalny, dla którego ustawiamy offset 2,5 V i amplitudę 50 mV. Konieczne jest też ustawienie zakresów dla przebiegów amplitudy i fazy. W oknie „Units” ustawiamy Top=10 dB, Bottom=–50 dB, zaś w oknie „Phase” Offset=0° i Range=360°. Wyniki pomiarów częstotliwościowych przedstawiono na rysunku 20.
Podsumowanie
Artykuł nie wyczerpał tematyki związanej ze stabilnością układów elektronicznych. Właściwie ledwie ją musnęliśmy. Pozostało jeszcze sporo zagadnień do omówienia, ale założeniem tego cyklu było przedstawianie wielu zagadnień, a nie skupianie się na jednym. Może jeszcze kiedyś będzie okazja do powrócenia do tematu, na pewno jednak nie będziemy analizować marginesów fazy i wzmocnienia w kolejnym odcinku, mimo że zajmiemy się generowaniem sygnałów elektrycznych.
Jarosław Doliński, EP

 Zaloguj
Zaloguj