Obliczenia można podzielić na kolejne fazy. Pierwszą z nich są niewątpliwe obliczenia stałoprądowe: ustalanie napięć zasilających, dobieranie punktów pracy, sprawdzanie mocy wydzielanej na elementach czynnych itp. Kolejny krok to już obliczenia zmiennoprądowe, a więc dobieranie wszelkich pojemności i indukcyjności pod kątem spełnienia wymagań częstotliwościowych. Coraz częściej konstruktorzy, nawet zajmujący się elektroniką amatorsko, stosują na tym etapie symulacje komputerowe, które albo potwierdzają obliczenia papierowe, albo... wprowadzają nas w konsternację, pokazując zupełnie inne wyniki od zakładanych. Wiekopomne zasługi należy tu przypisać firmie Linear Technology, obecnie Analog Devices, która udostępniła darmowy, przy tym bardzo profesjonalny program symulacyjny LTspice. Można już nawet mówić, że obecnie stanowi on swego rodzaju standard wśród narzędzi wspomagających projektowanie układów elektronicznych. Doceniają to nawet różni producenci elementów elektronicznych, udostępniając modele LTspice'owe swoich wyrobów. Posiadając pewne doświadczenie w obsłudze LTspice'a, można wręcz zrezygnować z obliczeń papierowych, a dobór elementów wykonać jedynie poprzez symulacje. Trzeba natomiast pamiętać, że każda symulacja jest tak dobra, jak dobre są użyte w niej modele.
Wróćmy do spraw projektowych. W dużej części przypadków obliczenia zmiennoprądowe kończą ten etap projektowania układu. Na ogół pomijane są obliczenia i symulacje dotyczące szumów. Wyjątkiem są przypadki wykonywania projektów urządzeń audio lub precyzyjnych przyrządów pomiarowych. Pozostańmy więc przez chwilę na tym etapie. Oczywiście o szumach można napisać całą książkę, więc w jednym artykule ogólną teorię potraktujemy bardzo powierzchownie, a skupimy się raczej na obliczeniach. Przyjmijmy jeszcze założenie, że projektowane urządzenie będzie zbudowane w oparciu na wzmacniaczu operacyjnym.
Minimalna wiedza o szumach
Aby prawidłowo wykonać obliczenia szumów należy posiadać minimalną wiedzę na ich temat. Najważniejsze zagadnienia zostaną krótko omówione w dalszej części artykułu, natomiast do dokładnego zapoznania się z tematyką odsyłam do licznych materiałów dostępnych w sieci i literaturze drukowanej.
Zaczynamy od rodzajów szumów. Projektując urządzenie elektroniczne, należy rozpatrywać dwa rodzaje źródeł szumów. Są to szumy zewnętrzne, generowane poza urządzeniem, np. przez sieć zasilającą, przetwornice, radio itp. i szumy wewnętrzne, generowane przez elementy urządzenia. Nas będą interesować tylko szumy wewnętrzne, gdyż tylko te jesteśmy w stanie jakoś policzyć. Bierzemy więc pod uwagę:
- szum 1/f (często nazywany również szumem migotania (flicker noise),
- szum szerokopasmowy,
- szum prądowy,
- szum termiczny.
Załóżmy, że projektujemy urządzenie, w którym będzie zastosowany wzmacniacz operacyjny OP77. Zacznijmy od krótkiego przeglądu informacji istotnych z punktu widzenia analizy szumów, które są podawane w nocie katalogowej tego układu.
Na rysunku 1 przedstawiono wykres napięciowej gęstości szumu w funkcji częstotliwości. Jest to typowy kształt spotykany w notach każdego wzmacniacza operacyjnego ogólnego przeznaczenia. Zwróćmy uwagę na dwa zakresy (interesuje nas dolna krzywa przedstawiona na tym wykresie). Począwszy od najniższych częstotliwości (1 Hz na wykresie) do ok. 2,6 Hz, gęstość szumu maleje na wykresie liniowo. Pamiętajmy jednak, że oś pionowa ma skalę logarytmiczną. Ponieważ gęstość szumu maleje odwrotnie proporcjonalnie do częstotliwości, najczęściej szumowi takiemu nadaje się nazwę 1/f. Często jest on nazywany również szumem migotania albo szumem różowym. Po przekroczeniu częstotliwości ok. 2,6 Hz gęstość szumu praktycznie już nie zależy od częstotliwości, więc dla częstotliwości wyższych od 2,6 Hz mamy do czynienia z szumem szerokopasmowym lub białym. Częstotliwość 2,6 Hz wypada w punkcie przecięcia przedłużeń wykresu dla zakresu 1/f i szerokopasmowego.
Ujarzmianie pierwiastka z herca
Uważny Czytelnik na pewno zwrócił uwagę na wielkość fizyczną użytą na wykresie z rysunku 1 do opisu szumów. Szum jest zjawiskiem losowym, które można opisać jedynie metodami statystycznymi. Jeśli mówimy o szumie napięciowym, to rozumiemy, że mamy do czynienia z chaotycznymi zmianami tego napięcia w czasie. Trudno mówić, że szum ma jakąś konkretną częstotliwość, bardziej trafne będzie określanie pewnej umownej wielkości tego szumu, która odnosi się do konkretnego pasma częstotliwości. Mówimy zatem o gęstości szumu, czyli o jego "ilości" przypadającej na przyjęty zakres częstotliwości. Można się o tym bardzo łatwo przekonać samodzielnie, przeprowadzając pewien eksperyment z użyciem darmowego programu Audacity. Zachęcam do samodzielnego powtórzenia poniższego przykładu.
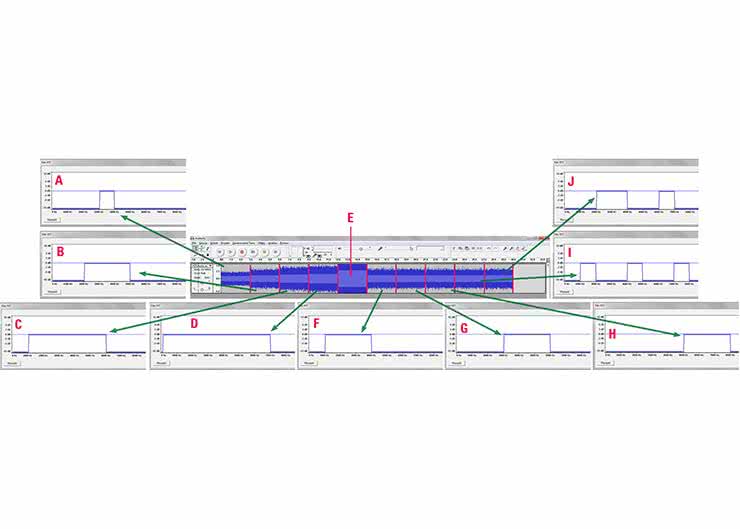
Zatem zaczynamy. Pierwszym krokiem jest wygenerowanie szumu - Audacity ma taką możliwość. Po wykonaniu polecenia "Generowanie Tonu V Biały Szum" (rysunek 2) zostanie wygenerowana 30-sekundowa ścieżka audio zawierająca biały szum. Należy zauważyć, że poziom sygnału jest stały dla całej ścieżki. Następnie będziemy ją dzielić na 3-sekundowe odcinki, w każdym z nich zastosujemy odmienne filtry. Zakładamy przy tym, że będzie nas interesować pasmo do ok. 8 kHz, tak abyśmy mieli pewność, że pasmo to przeniosą wszystkie urządzenia odsłuchowe i żebyśmy oczywiście sami byli w stanie wszystko usłyszeć. Wybieramy więc narzędzie "Zaznaczanie" (z przybornika w lewym górnym rogu ekranu) i przy naciśniętym lewym przycisku myszki przeciągamy kursor przez fragment wykresu od początku do 3 sekundy, po czym zwalniamy przycisk. Wybrany fragment jest zaznaczony na osi czasu w postaci szarego paska (rysunek 3).
Teraz zastosujemy filtr FFT, wybierając go komendą "Efekty → F iltr F FT...". D o precyzyjnego ustawienia charakterystyki filtru warto rozciągnąć okno "Filtr FFT" na całą szerokość ekranu (rysunek 4). Klikając na niebieską linię charakterystyki częstotliwościowej, wprowadzamy nowy jej punkt, który następnie można przesuwać w odpowiednie miejsce. W ten sposób można ukształtować żądaną charakterystykę filtru. Utwórzmy więc filtr, który będzie maksymalnie tłumił wszystkie częstotliwości od zera do 3000 Hz i od 4000 do końca pasma. Pasmo od 3000 do 4000 Hz powinien przenosić bez tłumienia (0 dB). Następnie na tej samej zasadzie dla kolejnych 3-sekundowych przedziałów budujemy filtry pasmowoprzepustowe (rysunek 5): 2000...5000 (b), 1000...6000 (c), 0...7000 (d). Odcinek od 12 do 15 sekundy (e) pozostawiamy bez filtru, a w następnych 3-sekundowych przedziałach definiujemy jeszcze: filtr od 1000...4000 Hz (f), 2000...6000 (g) i 5000...8000 Hz (h). Zauważmy, że filtry f, g i h filtrują różne fragmenty pasma, ale zawsze o szerokości 3 kHz.
Na zakończenie zbudujmy jeszcze dwa specyficzne filtry. Pierwszy z nich (i) będzie właściwie połączeniem filtrów o pasmach 1000...2000 Hz, 4000...5000 Hz i 7000...8000 Hz, a więc łączna szerokość takiego filtru jest równa też 3 kHz. I na zakończenie jeszcze jedna kombinacja (j): 2000...4000 Hz i 6000...7000 Hz, również o łącznej szerokości 3 kHz. Po wykonaniu tej mozolnej pracy możemy już przystąpić do odsłuchu, najlepiej za pomocą słuchawek. Zalecam przy tym ustawienie minimalnego poziomu głośności w komputerze, a następnie zwiększenie go zgodnie z własną potrzebą. W dalszych pomiarach poziomu tego już nie zmieniamy.
No i teraz wnioski. Zauważmy, że filtry od "a" do "d" charakteryzowały się coraz większymi szerokościami pasma przepustowego. Pomiar "e" przebiegał bez użycia filtru. Subiektywne wrażenie odsłuchowe jest takie, jakby głośność zwiększała się dla każdego kolejnego przedziału. Widać to również wyraźnie na wykresie czasowym programu Audacity i jego wskaźnikach poziomu. W kolejnych trzech przypadkach f...h zostały zastosowane filtry o tej samej szerokości pasma przepustowego (3 kHz), lecz o innych częstotliwościach środkowych. Wrażenia odsłuchowe są teraz nieco inne. Owszem, zmienia się barwa dźwięku, ale głośność pozostaje niezmienna. Już po wykonaniu tych eksperymentów można nieśmiało wysnuć wniosek, że faktycznie "ilość" szumu zależy od pasma częstotliwości. Utwierdzamy się w tym przekonaniu po odsłuchaniu przypadków "i" i "j". W każdym z nich występuje kilka zakresów częstotliwości o łącznej (zsumowanej) szerokości równej 3 kHz. Subiektywnie odbierana głośność i w tych eksperymentach nie ulega zmianie. Ucho jest niezłym miernikiem tego szumu, lecz jak ktoś nie dowierza własnym zmysłom, a dysponuje odpowiednim przyrządem pomiarowym, np. miernikiem True RMS, może się o tym przekonać. Ważne jest jednak, aby był to miernik True RMS i aby miał wystarczające pasmo pomiarowe. Dobrym rozwiązaniem jest, jak zwykle w takich przypadkach, oscyloskop. Charakterystyki filtrów i przebieg czasowy z programu Audacity przedstawiono na rysunku 5.
Zastanówmy się jeszcze przez chwilę, jaki parametr mierzyliśmy uchem. Stosowane dotychczas pojęcie "ilość" było umowne, gdyż nie wiedzieliśmy właściwie, co miało ono oznaczać. Na podstawie przeprowadzonych eksperymentów możemy powiedzieć, że ta "ilość" to po prostu moc szumu, a ponieważ sprawdziliśmy, że moc zależy od pasma, w którym badamy szum, najbardziej trafne będzie wprowadzenie pojęcia "gęstości mocy szumu". Parametr ten określa moc szumu w ustalonym zakresie częstotliwości, a więc p=P/Δf, gdzie p - gęstość mocy, P - moc zmierzona w zakresie częstotliwości Δf. Gęstość mocy jest najczęściej wyrażana w podstawowych jednostkach wielkości użytych do definicji, a więc w watach na herc (W/Hz). W praktyce jednak dużo łatwiej jest mierzyć napięcie niż moc, więc w katalogach stosowana jest napięciowa gęstość szumu. Jak wiadomo, moc jest proporcjonalna do kwadratu napięcia, dokładnie:
Można zatem też mówić, że napięcie jest proporcjonalne do pierwiastka z mocy:
Na tej podstawie możemy wyrazić gęstość mocy zależnością:
gdzie:
p – gęstość mocy szumu,
P – moc,
Df – zakres częstotliwości,
U – napięcie skuteczne szumu,
R – rezystancja, na której wydzielana jest moc.
Biorąc to pod uwagę oraz pamiętając o zależności 2, można napisać również zależność na napięciową gęstość szumu:
gdzie:
u – napięciowa gęstość szumu,
p – gęstość mocy szumu,
R – rezystancja, na której wydziela się moc,
Df – zakres częstotliwości,
U – wartość skuteczna napięcia szumu.
Jak widać, plącząca się rezystancja została wyrugowana i w ostatecznym wzorze na napięciową gęstość szumu występuje tylko skuteczne napięcie szumu i zakres częstotliwości pod pierwiastkiem. Stąd właśnie bierze się ten nieszczęsny pierwiastek z herca. Swoją drogą, ciekawe, dlaczego ludzi dziwi taka nietypowa jednostka i nie mogą sobie uzmysłowić jej sensu fizycznego, natomiast nikogo nie dziwi, na przykład - sekunda do kwadratu w mianie przyśpieszenia. A teraz krótka zagadka dla Czytelników: jaką, dobrze znaną wielkość fizyczną można wyrazić mianem: m-2·kg-1·s4·A2? Szczególnie tajemniczo wygląda ten kilogram.
Pozostały do przedyskutowania jeszcze szumy termiczne i prądowe, ale wspomnimy o nich, wykonując już obliczenia wzmacniacza, który projektujemy.
Obliczenia szumów wzmacniacza
Obliczanie szumów projektowanego wzmacniacza jest zajęciem dość złożonym, wieloetapowym. Poniższy opis można traktować jako uniwersalny algorytm stosowany do rozwiązywania takich zadań.
Obliczenia podzielimy więc na kilka kroków. Schemat projektowanego układu przedstawiono na (rysunku 6). Jest to wzmacniacz w konfiguracji z wejściem nieodwracającym.
Zagadnienie I. Obliczenie szumu szerokopasmowego
Krok 1. Wzmocnienie szumów. Jest ono równe wzmocnieniu wzmacniacza w konfiguracji z wejściem nieodwracającym, które jest równe:
Krok 2. Określenie częstotliwości granicznej dla wzmocnienia jednostkowego. W katalogach parametr ten jest oznaczany jako GBP (Gain Bandwidth Product) lub BW (Bandwidth). Można go odczytać z danych podawanych w tabeli (rysunek 7) lub z wykresu wzmocnienia wzmacniacza w otwartej pętli (rysunek 8).
Niestety, czasami zdarzają się pewne różnice między tabelami i wykresami. W zasadzie w takich sytuacjach należałoby brać parametr odpowiadający gorszemu przypadkowi. Ponieważ z tabeli wynika, że częstotliwość graniczna jest równa 600 kHz a z wykresu ok. 430 kHz, wybieramy daną podawaną w tabeli, czyli:
fBW=600 kHz
Krok 3. Obliczenie częstotliwości 3 dB (fn) wzmacniacza na podstawie wykresu z rysunku 8 na naniesionej krzywej dla wzmocnienia 101 V/V=ok. 40 dB
fn=6,4 kHz
Krok 4. Obliczenie znormalizowanego pasma wzmacniacza BWn. Częstotliwość górna jest wyznaczana przez przemnożenie częstotliwości 3 dB (fn) przez współczynnik kn, który dla nachylenia charakterystyki 20 dB/dek jest równy 1,57
BWn = 6,4k ⋅ 1,57 = 10,05 kHz
Spadek charakterystyki o 3 dB jest pewną wielkością, która umożliwia ilościową ocenę przenoszenia wzmacniacza. Nie oznacza to jednak, że po przekroczeniu poziomu 3-decybelowego wzmacniacz już w ogóle nie wzmacnia. Widać to zresztą wyraźnie na wykresie. Oczywiste zatem staje się, że część charakterystyki po prawej stronie od punktu, w którym opada ona o 3 dB, trzeba również uwzględnić. Efektywna szerokość pasma będzie więc większa. Z dokładniejszych analiz, których nie będziemy tu przytaczać, wynika, że do uzyskania znormalizowanego pasma konieczne jest przemnożenie pasma fBW przez współczynnik 1,57. Jak już było wspomniane, współczynnik ten odpowiada nachyleniu charakterystyki z szybkością 20 dB/dekadę, co jest wartością typową.
Krok 5. Obliczenie szerokopasmowego napięcia szumu enBB. Jak już zdążyliśmy się przyzwyczaić, chodzi o wartość skuteczną tego napięcia. enBB jest równe:
Parametr eBB odczytujemy z wykresu wejściowej napięciowej gęstości szumu wzmacniacza OP77 (rysunek 1). Ostatecznie mamy:
Otrzymaliśmy pierwszy składnik szumu, który posłuży dalej do obliczenia szumu całkowitego.
Zagadnienie II. Obliczenie szumu 1/f
Krok 6. Obliczenie rozpoczynamy od znormalizowanego dla 1 herca szumu 1/f (efnorm). Parametr ten pozwoli nam następnie obliczyć szum dla dowolnego zakresu częstotliwości. Wartość efnorm odczytujemy z wykresu przedstawionego na rysunku 1 dla częstotliwości 1 Hz. W naszym przypadku eat_f=13,3 nV/√Hz, a szum znormalizowany wynosi:
Krok 7. Mając szum znormalizowany, można obliczyć szum 1/f dla dowolnego pasma. Są do tego potrzebne dwa parametry: fH - częstotliwości górna wyznaczona przez znormalizowane pasmo wzmacniacza, a więc uwzględniająca załamanie charakterystyki częstotliwościowej oraz fL - dolna częstotliwość przyjmowana zwykle jako 0,1 Hz. Ostatecznie więc skuteczne napięcie szumu 1/f jest równe:
Krok 8. Obliczenie całkowitego szumu napięciowego ( 1/f i szerokopasmowego)
Zagadnienie III. Obliczenie szumu prądowego
Dla szumu prądowego rozpatrywany jest tylko szum szerokopasmowy. Konieczne natomiast będzie przeliczenie go na jego napięciowy odpowiednik. Ale po kolei.
Krok 11. Obliczenie szerokopasmowego szumu prądowego. W katalogach raczej rzadko prądowa gęstość szumu podawana jest na wykresach. Odpowiednich danych należy szukać raczej w tabelach i jak zwykle producenci nie ułatwiają życia klientom, stosując różne nazewnictwo. Najlepiej kierować się po mianach parametrów. Mówimy o gęstości szumu, więc należy szukać jednostek pA/√Hz czy nawet fA/√Hz. Często wartość ta jest podawana dla trzech częstotliwości. W naszym przykładzie tak właśnie jest (rysunek 9). W nocie katalogowej wzmacniacza OP77 interesujący nas parametr ma dość oczywistą nazwę: "Input noise current density". Z ciekawości wykonałem odręczny wykres przedstawiony na rysunku 10. Wartość skuteczna prądowego szumu szerokopasmowego jest obliczana z zależności:
- gdzie iBB jest wartością odczytaną z tabeli (rysunek 9).
Krok 12. Obliczenie całkowitego szumu prądowego RMS. Ponieważ dla szumu prądowego rozpatrywany jest tylko szum szerokopasmowy, obowiązuje zależność:
in = inBB = 12,03 pARMS
Krok 13. Wyniki prowadzonych obliczeń będą weryfikowane poprzez symulacje i pomiary zmontowanego rzeczywistego urządzenia. Mogą być do tego wykorzystywane takie przyrządy jak: mierniki True RMS, oscyloskopy lub analizatory widma. Byłoby raczej trudno mierzyć szum prądowy, dlatego musi on być przeliczony na szum napięciowy. Jest do tego potrzebna rezystancja zastępcza Req, na której będzie się odkładało napięcie pochodzące od szumu prądowego. Tą rezystancją jest równoległe połączenie rezystorów R1 i R2, więc Req=0,99 kΩ, a napięciowy szum stanowiący odpowiednik szumu prądowego jest równy:
en_i = in ⋅ Req = 12,03p ⋅ 0,99k = 11,9 nVRMS
Zagadnienie IV. Szum termiczny
Krok 14. Obliczenie rezystancji wypadkowej. Wprawdzie rezystancja ta była już liczona wcześniej, ale powtarzamy te obliczenia, gdyż rezystancja wypadkowa decyduje o szumie termicznym. Szum termiczny z definicji jest wytwarzany na wszystkich rezystancjach występujących w obwodzie. Można więc zadać teoretyczne pytanie: czy kondensatory i cewki mają również wpływ na szum termiczny. Odpowiedź jest dość niejednoznaczna. Gdybyśmy podchodzili do problemu bardzo teoretycznie, to owszem, musielibyśmy uwzględniać również wpływ rezystancji szeregowej kondensatora, a nawet szum wywołany stratami w dielektryku. Podobnie rezystancja cewki jest również źródłem szumu termicznego, jednak zarówno wpływ kondensatorów, jak i cewek na szum całkowity jest pomijalnie mały, i mówiąc potocznie - szkoda sobie zawracać nim głowę.
Przypomnijmy więc - rezystancja wypadkowa jest równa:
Krok 15. Obliczenie szumu termicznego generowanego przez rezystory. Nie wnikając w teorię, korzystamy z podanego niżej znanego wyrażenia na szum termiczny. Uwzględnia on stałą Boltzmanna (k), temperaturę bezwzględną w kelwinach (T, przyjmuje się zwykle 25°C, czyli 298 K ), rezystancję w ypadkową oraz znormalizowane pasmo:
Zagadnienie V. Obliczenie całkowitego szumu wyjściowego
Pamiętamy, że licząc napięciowe szumy wszystkich rodzajów, rozpatrywaliśmy wartości skuteczne. Nadszedł wreszcie moment, w którym możemy je zsumować. Jak pamiętamy z podstaw elektrotechniki, napięć skutecznych nie można sumować algebraicznie, trzeba zastosować sumowanie geometryczne. Przypomnijmy, że chodzi o szum napięciowy będący sumą szumu 1/f i szumu szerokopasmowego, szum napięciowy pochodzenia prądowego i szum termiczny. Ostatecznie więc wejściowy szum całkowity jest równy:
Zagadnienie VI. Obliczenie szumu wyjściowego
Należy jeszcze raz zwrócić uwagę na to, że policzony szum en_in jest szumem wejściowym. Takie podejście do obliczeń jest bardzo korzystne, gdyż uwalania nas od uwzględniania wzmocnienia wzmacniacza we wszystkich dotychczasowych krokach. Chociaż nazewnictwo m.in. parametrów szumowych w katalogach różnych producentów jest, można powiedzieć, dowolne, to parametry te zawsze są odnoszone do wejścia wzmacniacza. Oczywiście mało kto jest zainteresowany szumami na wejściu, ale żeby uzyskać szumy wyjściowe, wystarczy pomnożyć napięcie wejściowe szumu przez wzmocnienie układu, równoważne wzmocnieniu szumów. W naszym przykładzie jest ono równe: Kun=101 V/V. Zatem całkowity napięciowy szum wyjściowy (RMS) jest równy:
en_out = en_in ⋅ Kun = 1079[nVRMS] ⋅ 101[V/V] = 109,0 µVRMS
Czy to już koniec obliczeń? Można powiedzieć, że w zasadzie tak, ale należałoby się zastanowić nad jakąś metodą weryfikacji tych obliczeń. W związku z tym, że mamy do czynienia z wartością skuteczną, najlepszy byłby miernik napięcia True RMS. Musimy jednak pamiętać, że pasmo, w którym dokonujemy pomiaru, jest równe ok. 10 kHz, a często w takich pomiarach jest znacznie szersze. Użyty w przykładzie wzmacniacz OP77 ma małą częstotliwość jednostkową (GBP), co w konsekwencji powoduje znaczne ograniczenie pasma roboczego. Popularne multimetry mogą sobie nie poradzić, potrzebny byłby woltomierz True RMS wyższej klasy. Rozwiązaniem może być oczywiście oscyloskop. Nawet przyrządy z najniższej półki cenowej powinny nadawać się do pomiaru. Najlepiej gdyby w zestawie pomiarów automatycznych miał opcję pomiaru wartości skutecznej napięcia. Gdyby tak nie było, pozostanie nam mierzyć napięcie międzyszczytowe szumu bezpośrednio z oscylogramu. Trzeba będzie jednak jakoś odnieść ten wynik do obliczonego napięcia skutecznego. Na podstawie analizy statystycznej szumu, przy założeniu, że jest to szum gaussowski, można napisać zależność:
en_out_pp = en_out ⋅ 6 = 109[µVRMS] ⋅ 6 = 654 µVpp
Współczynnik 6 wynika ze statystycznej zależności pomiędzy wartością RMS i międzyszczytową szumu. Dla takiego współczynnika mamy 99,7% pewności wychwycenia wszystkich wartości szczytowych.
Teraz już możemy odetchnąć. Analiza została zakończona. Czy 654 mikrowolty peek-to-peek szumu to dobry wynik? Nawet bardzo dobry, ale to pasmo... No cóż, coś za coś.
Weryfikacja
Tak naprawdę zweryfikować powyższe obliczenia mogą jedynie pomiary wykonane na urządzeniu rzeczywistym. Ale i tu nie będziemy mieli 100-procentowej pewności co do wyniku. Zbyt wiele czynników wpływa na to, co odczytujemy z przyrządów pomiarowych. Pamiętajmy, że mamy do czynienia z ekstremalnie niskimi poziomami sygnałów i w niezbyt sprzyjających, za to bardzo prawdopodobnych okolicznościach może się zdarzyć, że szumy mierników będą większe od szumów mierzonych. Producenci, opracowując dane katalogowe radzą sobie z tymi trudnościami, ale w warunkach amatorskich może to być bardzo trudne. Ja, w każdym razie, nie podejmuję się przeprowadzenia stosownych pomiarów. Pozostaje mi jedynie symulacja za pomocą programu LTspice.
Kubeł zimnej wody
W tym miejscu musimy wrócić do sentencji wypowiedzianej na początku, mówiącej, że symulacja jest tak dobra, jak dobre są użyte w niej modele. Już na początku okazało się, że są różnice między LTspice'ową symulacją a danymi katalogowymi. Widać ją na charakterystyce częstotliwościowej w otwartej pętli. Z danych katalogowych wynika, że maksymalne wzmocnienie powinno w takich warunkach być równe nieco ponad 140 dB, gdy tymczasem symulacja daje wynik... zaledwie 70 dB (rysunek 11a). To aż 2-krotnie mniej i to w skali logarytmicznej!. Na szczęście parametr ten nie ma większego znaczenia w naszych rozważaniach. Częstotliwość dla wzmocnienia 0 dB mniej więcej zgodziła się z parametrem katalogowym. Schemat użyty do tego wirtualnego pomiaru przedstawiono na rysunku 11c.
Na rysunku 12 przedstawiono natomiast pomiar szumu z użyciem funkcji .noise programu LTspice. Daje ona wprawdzie napięciową gęstość widmową szumu występującego na wyjściu układu, lecz za pomocą ukrytej komendy (Ctrl + kliknięcie lewym przyciskiem myszki na nazwie wykresu) można przeprowadzić całkowanie tej gęstości w zakresie częstotliwości obejmowanych przez wykres. Daje to oczywiście w wyniku skuteczne napięcie szumu w tymże zakresie. Wynik: 88,249 µV wobec 109 µV wynikających z obliczeń. Bez pomiaru trudno przyjąć, która z powyższych wartości jest bliższa prawdzie. Jeśli uznamy, że obliczenia są prawidłowe, to błąd względny symulacji wynosi ok. 24%, a wynik jest zawyżony. Jeśli natomiast przyjmiemy, że to wynik symulacji jest bliższy prawdzie, wówczas błąd obliczeń wynosi ok. 19% i jest zaniżony. Wniosek jest taki, że zarówno do obliczeń, jak i do symulacji należy podchodzić z umiarkowanym zaufaniem. Trzeba pamiętać, że zarówno w obliczeniach, jak i w symulacji wynik wyraźnie zależy od przyjętego pasma, co zresztą stanowi istotę szumu. Co o tym myśleć? Czy należy się z takich rezultatów cieszyć, czy raczej smucić? Czy można uznać, że wyniki mieszczą się w tzw. inżynierskiej dokładności. Zapraszam do dyskusji. A może ktoś pokusi się zbudować i zmierzyć nasz układ.
Jarosław Doliński, EP
Źródła:
- Art Kay, "Operational amplifier noise - Techniques and tips for analyzing and reducing noise".

 Zaloguj
Zaloguj